Database Input Issues

This was a sample presentation which I created at my workplace to present Database security issues. Most of the content is taken from the book Writing Secure code. Hope it is helpful to someone.

Number to word converter

Q: Take a number and give the equivalent number in British English words e.g.

1 = one

21 = twenty one

105 = one hundred and five

56945781 = fifty six million nine hundred and forty five thousand seven hundred and eighty one

etc.. up to 999,999,999 without using a tokenizer, or any external libraries

Working Code:

import java.text.DecimalFormat;

public class NumberToWord {

    private static final String[] tensWords = { "", " ten", " twenty",
            " thirty", " forty", " fifty", " sixty", " seventy", " eighty",
            " ninety" };

    private static final String[] words = { "", " one", " two", " three",
            " four", " five", " six", " seven", " eight", " nine", " ten",
            " eleven", " twelve", " thirteen", " fourteen", " fifteen",
            " sixteen", " seventeen", " eighteen", " nineteen" };

    // Convert Number to word which is less than one thousand   
    private static String convertLessThanOneThousand(int number) {
        String thousandWord;

        if (number % 100 < 20) {
            thousandWord = words[number % 100];
            number /= 100;
        } else {
            thousandWord = words[number % 10];
            number /= 10;

            thousandWord = tensWords[number % 10] + thousandWord;
            number /= 10;
        }
       
        if (number == 0)
            return thousandWord;
       
        return words[number] + " hundred" + thousandWord;
    }

   
    //Converts any number to word between 0 to 999 999 999 999 billions millions
    public static String convertNumberToWord(long number) throws Exception{

        if(number < 0)
        {
            throw new Exception("Negative numbers not supported");
        }
       
        if (number == 0) {
            return "zero";
        }

        String snumber = Long.toString(number);
        if(snumber.length() > 13)
        {
            throw new Exception("Numbers greater than 999 billion are not supported");
        }

        // pad with "0"
        String mask = "000000000000";
       
        // DecimalFormat converts 50 to 000000000050 based on the given mask
        DecimalFormat df = new DecimalFormat(mask);
        snumber = df.format(number);

        StringBuilder result = new StringBuilder();

        // XXXnnnnnnnnn
        int billions = Integer.parseInt(snumber.substring(0, 3));
        // nnnXXXnnnnnn
        int millions = Integer.parseInt(snumber.substring(3, 6));
        // nnnnnnXXXnnn
        int hundredThousands = Integer.parseInt(snumber.substring(6, 9));
        // nnnnnnnnnXXX
        int thousands = Integer.parseInt(snumber.substring(9, 12));

        String wordBillions;
        switch (billions) {
        case 0:
            wordBillions = "";
            break;
        case 1:
            wordBillions = convertLessThanOneThousand(billions) + " billion";
            break;
        default:
            wordBillions = convertLessThanOneThousand(billions) + " billion";
        }

        result.append(wordBillions);

        String wordMillions;
        switch (millions) {
        case 0:
            wordMillions = "";
            break;
        case 1:
            wordMillions = convertLessThanOneThousand(millions) + " million";
            break;
        default:
            wordMillions = convertLessThanOneThousand(millions) + " million";
        }

        result.append(wordMillions);

        String wordHundredThousands;
        switch (hundredThousands) {
        case 0:
            wordHundredThousands = "";
            break;
        case 1:
            wordHundredThousands = "one thousand ";
            break;
        default:
            wordHundredThousands = convertLessThanOneThousand(hundredThousands)+ " thousand";
        }

        result.append(wordHundredThousands);

        result.append(convertLessThanOneThousand(thousands));

        return result.toString();
    }

    public static void main(String[] args) {
       
        String word = "";
        try {
            word = NumberToWord.convertNumberToWord(999999999999L);
        } catch (Exception e) {
            System.out.println("error: "+e.getMessage());
        }
        System.out.println(word);
    }

}

Serializing a binary tree

Q: Design an algorithm and write code to serialize and deserialize a binary tree.

Advantages of serialization/deserialization include storing a binary into and restoring it for a later point of time, transmitting the tree over a network from one computer and load it in another computer.

One approach for this problem could be the nodes with NULL values using some kind of sentinel so that later nodes can be inserted In correct place while deserialization. Lets use the sentinel as # and we will use preorder traversal here serialization.

Assume we have a binary tree below:

The preorder traversal of the above tree can be written as 

30 10 50 # # # 20 45 # # 35 # #

Finding Unique number

Q: You are given an array that contains integers. The integers content is such that every integer occurs 3 times in that array leaving one integer that appears only once.
Fastest way to find that single integer

eg:
Input: {1,1,1,3,3,3,20,4,4,4};

Answer: 20

The logic is similar to finding the element which appears once in an array - containing other elements each appearing twice. There we do XOR all the elements and the result will be the unique number.

To apply the similar logic to this problem we maintain 2 variables

ones - This variable holds XOR of all the elements which have appeared only once.
twos - This variable holds XOR of all the elements which have appeared twice.

The algorithm goes as follows…

1. A new number appears - It gets XOR' ed to the variable "ones".
2. A number gets repeated(appears twice) - It is removed from "ones" and XOR'd to the
variable "twos".
3. A number appears for the third time - It gets removed from both "ones" and "twos".

The final answer will be in "ones" as it holds the unique element.

Working Java code:

Multiplication of numbers

Q: There is an array A[N] of N numbers. You have to compose an array Output[N] such that Output[i] will be equal to multiplication of all the elements of A[N] except A[i]. For example Output[0] will be multiplication of A[1] to A[N-1] and Output[1] will be multiplication of A[0] and from A[2] to A[N-1]. Solve it without division operator and in O(n).

A: {4, 3, 2, 1, 2}
OUTPUT: {12, 16, 24, 48, 24}

Since we should not use, division operator, Brute force approach would be O(n^2)

Other approach is by storing the result temporarily in an array.

Let’s define array B where element B[i] = multiplication of numbers from A[0] to A[i]. For example, if A = {4, 3, 2, 1, 2}, then B = {4, 12, 24, 24, 48}. Then, we scan the array A from right to left, and have a temporary variable called product which stores the multiplication from right to left so far. Calculating OUTPUT[i] is straight forward, as OUTPUT[i] = B[i-1] * product.

Above approach requires O( n ) time and also O( n ) space.

We can actually avoid the temporary array. We can have two variables called left and right, each keeping track of the product of numbers multiplied from left->right and right->left.

Robot Unique Paths

Q: A robot is located at the top-left corner of a m x n grid. The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid. How many possible unique paths are there?

We can solve this problem using backtracking approach.

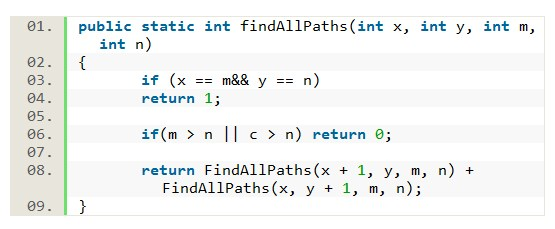
Other approach is using dynamic programming with memorization.

Longest Palindrome in a string

Brute force Algorithm.

1. Have 2 for loops
   for i = 1 to i less than array.length -1
   for j=i+1 to j less than array.length
2. This way you can get substring of every possible combination from the array
3. Have a palindrome function which checks if a string is palindrome
4. so for every substring (i,j) call this function, if it is a palindrome store it in a string variable
5. If you find next palindrome substring and if it is greater than the current one, replace it with current one.
6. Finally your string variable will have the answer

Brute force approach for this problem takes O(n3) time.

Another approach is

1. Reverse the string and store it in different string
2. Now find the largest matching substring between both the strings

This too will take O(n2) time

We can solve this problem using suffix trees, but constructing the suffix tree itself seems to be more complex in terms of both time and space complexity.

We can solve this problem using a better approach which will revolve around with a center for every single character.

For each position in the string we store an upper and lower pointer that tracks the upper and lower bounds of the largest palindrome centered at that position.

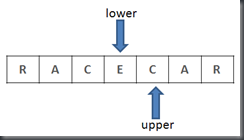
For instance, position 2 in the string "racecar" would start as:

At this point, the longest known palindrome at position 2 is the single character 'c'. We then increment the upper pointer and decrement the lower pointer and compare their respective values.

Since the upper and lower values are not the same, we stop and now know that the longest palindrome centered at position 2 is 'c'. We then start the process again at the next string position, 3.

We increment and decrement the upper and lower pointers and see that they are equal. Our current longest palindrome centered at position 3 is now 'cec'.

Since they were equal, we increment and decrement the pointers again and see that they are still equal. Our new longest palindrome centered at position 3 is now 'aceca'.

We continue incrementing and decrementing the upper and lower pointers until they don't match or they hit one of the ends of the string.

Since our pointers are equal, we increment and decrement them again. We hit an end of the string and the pointers are equal so we know that our longest palindrome centered at position 3 is 'racecar'.

We're done with position 3 and continue this same process again at position 4. We'll do this until we've covered every position in the string.

NOTE: We initially assumed that the palindrome had an odd length. This algorithm works for even palindromes as well. The only change we make is that when we initialize the pointers, instead of having the lower and upper pointer point to the same position we have the upper pointer point at the next position. Everything else with the algorithm remains the same. i.e. The initial pointers for an even palindrome 'centered' at position 3 would look like:

Runtime:

Worst-Case: O(N^2)

Best-Case: O(N)

The worst case is achieved when the string is a single repeated character because every substring is a palindrome.

The best case is achieved when the string contains no palindromes.

Typically if a string only contains a single palindrome (the fewer the better), the closer to O(N) it will run. This is because every time it checks a position in the string, it checks the character before and after that position, and if they don't match then it stops looking for the palindrome. Positions in the string can be discarded after only one lookup if that position doesn't have a palindrome, so if there are no palindromes you only do N comparisons.

JavaCode:

3 sum and 2 sum problem

Q: Given an integer x and an unsorted array of integers, describe an algorithm to determine whether two of the numbers add up to x.

If we have hash table, we can just check for every number ‘a’, if x-‘b’ is present in hash table. This takes O( n ) with constant space for hashtable. What if the interviewer hates the hashtable.

Sort the array. Then, keep track of two pointers in the array, one at the beginning and one at the end. Whenever the sum of the current two integers is less than x, move the first pointer forwards, and whenever the sum is greater than x, move the second pointer backwards. This solution takes O(n log n) time because we sort the numbers.

Another approach for this problem could be…

Create a binary search tree containing x minus each element in the array. Then, check whether any element of the array appears in the BST. It takes O(n log n) time to create a binary search tree from an array, since it takes O(log n) time to insert something into a BST, and it takes O(n log n) time to see if any element in an array is in a BST, since the lookup time for each element in the array takes O(log n). Therefore step one takes O(n log n) time and step two takes O(n log n) time, so our total running time is O(n log n).

Variations for this problem would be, find three integers a,b,c in the array such that a+b=c

This will  take O(n²) time complexity.

Other variation is Find three integers a,b,c in the array such that a+b+c =0

Big File containing billions of numbers

Q: There is big file containing billions of numbers. How do we find maximum 10 numbers from those files?

Priority queue is the best data structure to answer such question. Of course loading all the data and building the heap is not such a good idea. Main challenge is how do we manage chunks of data in memory and arrive at the solution.

Divide the data into some sets of 1000 elements, make a heap of them and take 10 element from each heap one by one. Finally sort all the sets of 10 elements and take top 10 among those. But where do we store 10 element from each heap which may itself require large amount of memory as we have billions of numbers.

Reuse top 10 elements from earlier heap in subsequent elements can solve this problem. Take first block of 1000 elements and subsequent blocks of 990 elements. The last set of 990 elements or less than that and taking top 10 elements from the final heap will fetch you the answer.

Time Complexity would be O( (n/1000)*(complexity of heapsort of 1000 elements) = O( n )

Median of two sorted arrays

This question is similar to the previous question which can solved in O(logn) using binary search approach. Lets see the algorithm….

Algorithm
1.Let the two arrays be a1,a2 with n elements each with n elements
2.Let med1 and med 2 be the medians of two arrays respcetively
3.if med1==med2 means the required median is med1(or med2)
4.if med1 < med2 that means the median can either lie in upper half of a1 or lower half  of a2     5.if med1 >med2 that means the median can be in lower half of of a1 or upper half of a2
we continue this process until two elements are present in the array
if two elements are present in the array then we calculate the median as follows
median_required = (max(a1[0],a2[0])+min(a1[1]+a2[1])) /2

Kth Smallest element

Q: Given two sorted arrays A, B of size m and n respectively. Find the k-th smallest element in the union of A and B. You can assume that there are no duplicate elements.

One approach we could think of is merge both arrays and the k-th smallest element could be accessed directly. Merging would require extra space of O(m+n). The linear run time is pretty good, but could we improve it even further?

Another approach is using two pointers, you can traverse both arrays without actually merging them, thus without the extra space. Both pointers are initialized to point to head of A and B respectively, and the pointer that has the larger of the two is incremented one step. The k-th smallest is obtained by traversing a total of k steps.

We can solve this problem in logarithmic time in O(lg m + lg n) using binary search approach.

We try to approach this tricky problem by comparing middle elements of A and B, which we identify as A_i and B_j. If A_i is between B_j and B_j-1, we have just found the i+j+1 smallest element. Therefore, if we choose i and j such that i+j = k-1, we are able to find the k-th smallest element. This is an important invariant that we must maintain for the correctness of this algorithm.

Maintaining the invariant
    i + j = k – 1,

If B_j-1 < A_i < B_j, then A_i must be the k-th smallest,
or else if A_i-1 < B_j < A_i, then B_j must be the k-th smallest.

We can make an observation that when A_i < B_j, then it must be true that A_i < B_j-1. On the other hand, if B_j < A_i, then B_j < A_i-1.

Using the above relationship, it becomes clear that when A_i < B_j, A_i and its lower portion could never be the k-th smallest element. So do B_j and its upper portion. Therefore, we could conveniently discard A_i with its lower portion and B_j with its upper portion.

Saving a Binary Search Tree to a File

Q: Describe an algorithm to save a Binary Search Tree (BST) to a file in terms of run-time and disk space complexity. You must be able to restore to the exact original BST using the saved format

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be “resurrected” later in the same or another computer environment.

Pre-order traversal is the perfect algorithm for making a copy of a BST. We can store the preorder traversal of the tree into File and then read it again to construct the tree. Assuming we have a file where the pre order traversal of the tree is written to it, We will now see how to read the file to construct that into BST.

Sorted List to Balanced Binary Search Tree

Q: Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

We can solve this problem using bottom up approach with recursion. We create nodes bottom-up, and assign them to its parents. The bottom-up approach enables us to access the list in its order while creating nodes.  Lets define the node structure for Binary Search Tree Node as follows

Below is the java code for converting a singly linked list to a balanced BST. The algorithm requires the list’s length to be passed in as the function’s parameters. The list’s length could be found in O(N) time by traversing the entire list’s once. The recursive calls traverse the list and create tree’s nodes by the list’s order, which also takes O(N) time. Therefore, the overall run time complexity is still O(N).

Word Suggest

This is general algorithm we use in search engines. Question is Given a dictionary suggest the words for a given misspelled word.

The word could be misspelled in either of the following 4 ways.

1. Transpositions: These are set of words where 2 adjacent characters in a word are trans positioned. Ex: hlelo –> hello . There are atmost n-1 trans positioned words for a given word.
2. Insertion: Word could be misspelled by inserting an extra character. Ex: helxlo –> hello There could be at the max n+1 words with this.
3. Substitution: Word could be misspelled by typing wrong character in place of another character. Ex: helxo –> hello . Max No. of Substituted words could 25 * ( n )
4. Omissions: These are set of words where a character is omitted Ex: hllo –> hello . Max No of omitted words could be 26*(n+1)

Lets code them now.

Suffix Trees

Suffix Tree for a String T is Trie like data that represents the suffixes of T. For example, if your word were bibs, you would create the following tree.

Suffix trees answers the queries related to one string. There are many applications of suffix trees. Some of them are..

1. String Matching and Pattern Matching algorithm
2. Longest Repeated SubString
3. Longest palindrome
4. Longest common substring
5. Longest Common prefix

Sample java Implementation of Suffix Tree:

String Search

Searching for a substring, pat[1..m], in txt[1..n], can be solved in O(m) time (after the suffix tree for txt has been built in O(n) time).

Longest Repeated Substring

Add a special ``end of string'' character, e.g. `$', to txt[1..n] and build a suffix tree; the longest repeated substring of txt[1..n] is indicated by the deepest fork node in the suffix tree, where depth is measured by the number of characters traversed from the root, i.e., `issi' in the case of `mississippi'. The longest repeated substring can be found in O(n) time using a suffix tree.

Longest Common Substring

The longest common substring of two strings, T1 and T2, can be found by building a generalized suffix tree for T1  and T2 : Each node is marked to indicate if it represents a suffix of T1 or T2 or both. The deepest node marked for both T1 and T2 represents the longest common substring.

Equivalently, one can build a (basic) suffix tree for the string T1$T2#, where `$' is a special terminator for T1 and `#' is a special terminator for T2. The longest common substring is indicated by the deepest fork node that has both `...$...' and `...#...' (no $) beneath it.

Palindromes

A palindrome is a string, P, such that P=reverse(P). e.g. `abba'=reverse(`abba'). e.g. `ississi' is the longest palindrome in `mississippi'.

The longest palindrome of T can be found in O(n) time, e.g. by building the suffix tree for T$reverse(T)# or by building the generalized suffix tree for T and reverse(T).

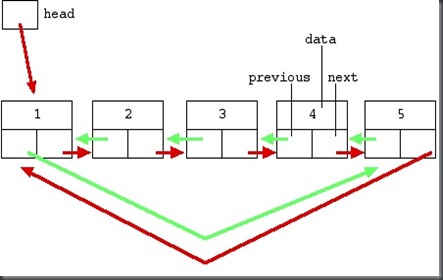
Linked List Question

Q: Given a linked list with two pointers in node structure where one points to the next node and the other pointer points to some random node in the linked list. Write a program to create a copy of this linked list

The above problem can be solved in O( n ) time and in constant space complexity. Assuming the Node Structure as following..

Algorithm:

1)[Merge listst]Create list B this way: for each NodeA in A create a NodeB in B , copy NEXT ptr to NodeB: NodeB{NEXT} = NodeA{NEXT} and change NEXT ptr in NodeA to this newly created node in B: NodeA{NEXT}=NodeB;
2) go through the list A (NB: you have to jump through the nodes of B!) and set NEXTRND ptr in next B nodes to the next ptrs after next_random nodes: NodeA{NEXT}{NEXTRND}=NodeA{NEXTRNF}{NEXT};
After that all NEXTRND nodes in list B will be pointing to correct nodes in B;
3) [Un-merge]. For each node in A and in NEXT node B set correct NEXT ptrs:
node=headA;
while(node){tmp = node{NEXT}; node{NEXT}=tmp?tmp{NEXT}:NULL; node=tmp;}
After this process all {NEXT} nodes in both lists A and B will be correct

Java Code:

Best days to sell and buy stock, if array of stock prices given

Q: Say you have an array for which the ith element is the price of a given stock on day i. If you were only permitted to buy one share of the stock and sell one share of the stock, design an algorithm to find the best times to buy and sell

Algorithm: Go through the array in order, keeping track of the lowest stock price and the best deal you've seen so far. Whenever the current stock price minus the current lowest stock price is better than the current best deal, update the best deal to this new value.

Working Java Code:

Arranging elements in specific order

n a given array of elements like [a1, a2, a3, a4, ..... an, b1, b2, b3, b4, ....... bn, c1, c2, c3, c4, ........ cn] without taking a extra memory how to merge like [a1, b1, c1, a2, b2, c2, a3, b3, c3, ............ an, bn, cn]

Triplet (x,y,z) whose distance is min

Given 3 sorted arrays (in ascending order). Let the arrays be A(of n1 length), B(of n2 length), C(of n3 length). Let x be an element of A, y of B, z of C. The distance between x, y and z is defined as the max(|x-y|,|y-z|,|z-x|). Find the tuple with the minimum distance?

Working java Code:

External Merge Sort

If data to be sorted doesn’t fit into main memory external sorting is applicable. External merge sort can be separated into two phases:

1. Create initial runs (run is a sequence of records that are in correct relative order or in other words sorted chunk of original file).
2. Merge created runs into single sorted file.

Let’s assume that M records at the same time are allowed to be loaded into main memory. One of the ways to create initial runs is to successively read M records from original file, sort them in memory and write back to disk.

The core structure behind this algorithm is priority queue. Taking one by one current minimum element out of the queue forms ordered sequence.

The algorithm can be described as follows:

1. Create two priority queues (that will contain items for current and next runs respectively) with capacity of M records.
2. Prefill current run priority queue from unsorted file with M records.
3. Create current run if there are elements in the current run priority queue:
   1. Take minimum element out of current run priority queue and append it to current run (basically write it to disk).
   2. Take next element from unsorted file (this is the replacement part of the algorithm) and compare it with just appended element.
   3. If it is less then it cannot be part of the current run (or otherwise order will be destroyed) and thus it is queued to the next  run priority queue.
   4. Otherwise it is part of the current run and it is queued to the current run priority queue.
   5. Continue steps 1 through 4 until current run priority queue is empty.
4. Switch current and next runs priority queues and repeat step 3.

At any given moment at most M records are loaded into main memory as single written element into current run is replaced with single element from unsorted file if any (depending on comparison it either goes into current or next run).

Next step is to merge created initial runs. For the merge step we will use simplified algorithm based on k-way merge.

1. Append created runs into a queue.
2. Until there are more than one run in the queue:
   1. Dequeue and merge K runs into a single run and put it into the queue.
3. Remaining run represents sorted original file.

K-Way Merge

The classic merge takes as input some sorted lists and at each step outputs element with next smallest key thus producing sorted list that contains all the elements of the input lists.

We can solve this problem using two ways.

Let the sorted arrays be A1, A2,...Ak

Way 1:
Merge (A1, A2), (A3, A4),...
Then there are k/2 sorted arrays now.
Repeat the above procedure to get the full array sorted. It is not always practical to have whole sequence in memory because of its considerable size nor to constraint sequence to be finite as only K first elements may be needed. Thus our algorithm must produce monotonically increasing (according to some comparison logic) potentially infinite sequence. This way wont work as the memory we can use is limited

Way 2:
Form a priority min heap from the first element of all the k arrays. Extract the min element. It is the min element among all the arrays. Now take the next element from the array from which the min element has come, and put it in the min heap. Repeat the procedure.

• The queue will hold non empty sequences.
• The priority of a sequence is its next element.
• At each step we dequeue out of the queue sequence that has smallest next element. This element is next in the merged sequence.
• If dequeued sequence is not empty it must be enqueued back because it may contain next smallest element in the merged  sequence.

Thus we will have queue of size that doesn’t exceed m (number of sequences) and thus making total running time O(n log m).  It works well with infinite sequences and cases where we need only K first elements and it fetches only bare minimum out of source sequences.

Selecting k smallest or largest elements

There are cases when you need to select a number of best (according to some definition) elements out of finite sequence (list). For example, select 10 most popular baby names in a particular year or select 10 biggest files on your hard drive.  

While selecting single minimum or maximum element can easily be done iteratively in O(n) selecting k smallest or largest elements (k smallest for short) is not that simple. One approach could be sort the elements and take the first k elements. But that requires O( nlogn) time.

Priority Queue can be used for better performance if only subset of sorted sequence is required. It requires O(n) to build priority queue based on binary min heap and O(k log n) to retrieve first k elements. Can we improve this further?

Quicksort algorithm picks pivot element, reorders elements such that the ones less than pivot go before it while greater elements go after it (equal can go either way). After that pivot is in its final position. Then both partitions are sorted recursively making whole sequence sorted. In order to prevent worst case scenario pivot selection can be randomized.

Basically we are interested in the k smallest elements themselves and not the ordering relation between them. Assuming partitioning just completed let’s denote set of elements that are before pivot (including pivot itself) by L and set of elements that are after pivot by H. According to partition definition L contains |L| (where |X| denotes number of elements in a set X) smallest elements. If |L| is equal to k we are done. If it is less than k than look for k smallest elements in L. Otherwise as we already have |L| smallest elements look for k - |L| smallest elements in H.

Working Java Code:

Queue based on single stack

Queue based on 2 stacks is generally what we usually know of and probably would be on our minds while answering such questions. We could solve the same using one stack and taking advantage of recursion. We will see how we can solve this with no additional storage.

Assume that items come out of stack in the order they must appear in the queue (FIFO). Choosing the opposite order is also possible however is not practical. To make it happen we simply need to make sure that items in the stack (LIFO) are placed in the opposite order. Items queued first must appear at the top of the stack. This basically means that in order to queue item all items must be popped, the item  pushed and then existent items pushed inversely to pop order. But we have no additional explicit storage requirement. Then store items implicitly through recursion.

Enqueue is a O(n) operation (where n is the number items in the stack). Dequeue and Peek is a O(1) operation.

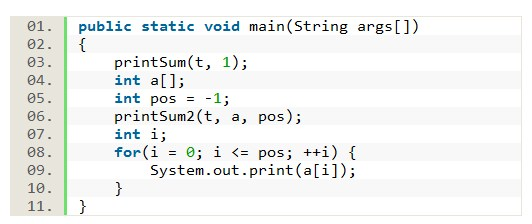
Cumulative sum of a tree at each node.

Q: Given a binary tree, print the sum( inclusive of the root ) of sub-tree rooted at each node in in-order

This question can be answered in two ways. We can do it using two passes with constant space of with one pass and O( n ) space.

Lets say the tree node is as follows

Converting a Tree to a double Linked List

Q: Write a program which will accept Binary Search Tree and convert it to a sorted Double Linked List.

For example if the Binary search tree is as shown below…

Then the converted doubly linked  list should be

Lets define the Node structure of the tree as follows

We can use recursive approach to solve this by just arranging the pointers..

Algorithm:

If tree is not empty

Convert Left Subtree to List and let hLeft point to it

Convert Right Subtree to List and left hRight point to it.

Append hLeft to root and then hRight

Working java Code:

Minimum window that contains all characters

Q: Find the smallest window in a string containing all characters of another string

Given set of characters P and string T find minimum window in T that contains all characters in P. Applicable solution is restricted to O(length(T)) time complexity. For example, given a string T “of characters and as” and set of characters T in a form of a string “aa s” the minimum window will be “and as”.

The problem can be broken into two parts:

• How to select window?
• How to check that selected window contains all characters from P?

Selecting every possible window (all unique pairs (i, j) where 0 <= i <= j < length(T)) will lead to solution worse than O(length(T)^2) because you still need to check if all characters from P are within selected window. Instead we will check every possible window ending position. Thus there are at least length(T) windows to consider.

Any feasible window has length equal to or greater than length(P). Performing recheck for any considered window will result in a solution no better than O(length(T)*length(P)). Instead we need to use check results from previous iteration.

Now we need to make sure that checking if a particular character is in P is done in an optimal way. Taking into account that a particular character may appear more than once and window thus must contain appropriate number of characters. We will use hash table to map unique characters from P to their count for fast lookup.

And now let’s tie all things together.

• Until reached the end of T move by one current window ending position.
• Append next character to the end of previous window which to this moment doesn’t contain all necessary characters. Char to count map is used to track the number of characters left to find. Basically if character is in P count is decremented. The number may become negative meaning that there are more than required characters.
• If unmatched character count goes to zero the window contains all required characters. However there may be redundant characters. Thus we try to compact current window. It is ok to do this as we are looking for minimum window and any window that is extended from this one won’t be better.
• Once window is compacted compare it with the minimum one and updated it if needed.
• If current window contains all the characters remove from it the first one simply by moving by one starting position to make sure that at each iteration previous window doesn’t contain all the characters (there is no point in appending new characters to a window that already contains all of the required ones).

Working Java code:

public static String findMinWindow(String t, String p)
    {
        // Create char to count mapping for fast lookup
        // as some characters may appear more than once
        HashMap<Character, Integer> charToCount = new HashMap<Character, Integer>();
        for (char c : p.toCharArray())
        {
            if (!charToCount.containsKey(c))
                charToCount.put(c, 0);
            charToCount.put(c, charToCount.get(c)+1);
        }
    
        int unmatchesCount = p.length();
        int minWindowLength = t.length() + 1,minWindowStart = -1;
        int currWindowStart = 0, currWindowEnd = 0;
        for (; currWindowEnd < t.length(); currWindowEnd++)
        {
            char c = t.charAt(currWindowEnd);
            // Skip chars that are not in P
            if (!charToCount.containsKey(c))
                continue;
            // Reduce unmatched characters count
            charToCount.put(c, charToCount.get(c)-1);
            if (charToCount.get(c) >= 0)
                // But do this only while count is positive
                // as count may go negative which means
                // that there are more than required characters
                unmatchesCount--;
    
            // No complete match, so continue searching
            if (unmatchesCount > 0)
                continue;
    
            // Decrease window as much as possible by removing
            // either chars that are not in T or those that
            // are in T but there are too many of them
            c = t.charAt(currWindowStart);
            boolean contains = charToCount.containsKey(c);
            while (!contains || charToCount.get(c) < 0)
            {
                if (contains)
                    // Return character to P
                    charToCount.put(c,charToCount.get(c)+1);
    
                c = t.charAt(++currWindowStart);
                contains = charToCount.containsKey(c);
            }
    
            if (minWindowLength > currWindowEnd - currWindowStart + 1)
            {
                minWindowLength = currWindowEnd - currWindowStart + 1;
                minWindowStart = currWindowStart;
            }
    
            // Remove last char from window - it is definitely in a
            // window because we stopped at it during decrease phase
            charToCount.put(c, charToCount.get(c)+1);
            unmatchesCount++;
            currWindowStart++;
        }
    
        return minWindowStart > -1 ?
               t.substring(minWindowStart, minWindowLength) : "";
    }

Every character is examined at most twice (during appending to the end and during compaction) so the whole solution has O(length(T)) time complexity assuming hash table lookup is O(1) operation.

Traversing binary tree in zig zag order

The question is we need to traverse binary tree level by level in such a way that traversal direction within level changes from level to level thus forming a spiral.

We’ll start with a well know problem of traversing binary tree level by level It can be done using queue. But this problem seems to be tricky. Its not the obvious approach. Instead of going with queue approach we can solve this problem using two stacks. Let us say the two stacks are curr Level and nextLevel. Next level is a set of child nodes from current level. We also need a variable to keep track of the current level’s order. If next level must be traversed from left to right we must first push right child node and then left and in opposite order if next level will be traversed from right to left we will push the left child first and then right child.

Working Java Code:

public void spiralOrderTraversal(BinaryTreeNode root)
    {
        Stack<BinaryTreeNode> currentLevel,nextLevel;
        BinaryTreeNode temp;
        int leftToRight = 1;
       
        if(root == null)
            return;
       
        currentLevel = new Stack<BinaryTreeNode>();
        nextLevel = new Stack<BinaryTreeNode>();
       
        currentLevel.push(root);
       
        while(!(currentLevel.isEmpty())
        {
            temp = currentLevel.pop();
            if(temp)
            {
                System.out.println(temp.data);
                if(leftToRight)
                {
                    if(temp.left)
                        nextLevel.push(temp.left);
                    if(temp.right)
                        nextLevel.push(temp.right);
                }
                else
                {
                    if(temp.right)
                        nextLevel.push(temp.right);
                    if(temp.left)
                        nextLevel.push(temp.left);
                }
               
                if(currentLevel.isEmpty())
                {
                    leftToRight = 1-leftToRight;
                    swap(currentLevel,nextLevel)
                }
            }
        }
    }

Longest consecutive elements sequence

For example, in {5, 7, 3, 4, 9, 10, 1, 6, 15, 1, 3, 12, 2, 11} longest sequence is {1, 2, 3, 4, 5,6}.

The first thing that comes into our mind is to sort given array in O(n log n ) and look for longest consecutive elements sequence. Can we do it in Linear time?

The next solution would be using bit vector indexed by numbers from original array. It may not be justified due to incomparable solution space and original array size (although time complexity is O(n)).

Lets see how to solve this problem in O( n ) time complexity with constant space assuming the hashtable has O(1) time complexity and constant space complexity.

By Knowing range boundaries we can definitely say what numbers are in there (for example, [1..3] contains 1, 2, 3). O(1) time complexity for range manipulation operations with O(1) space complexity for each range are the things we are looking for. We can do this using two hash tables:

• ‘low’ with range start numbers as keys and range end numbers as values
• ‘high’ with range end numbers as keys and range start numbers as values

For example, for a range [x..y] the tables will hold low[x] = y and high[y] = x. The algorithm looks the following:

• Scan original array and for each element:
  • If it already belongs to any range skip it
  • Otherwise create unit size range [i..i]
  • If there is a range next to the right [i+1.. y] merge with it to produce [i..y] range
  • If there is a range next to the left [x..i-1] merge with it as well (either [i..i] or merged [i..y] will be merged with [x..i-1])
• Scan through created ranges to find out the longest

Word in a Maze

Q: Given a puzzle of letters/ characters e.g.

a e r o p s
b h a r l s
w r i s l o
a s n k t q

Write a function to which this puzzle and a word will be passed to test whether that word exists in the puzzle or not.
e.g. rain and slow will return true. rain is present in the third column and slow in the third row wrapped around.

Algorithm:

Idea is for each element in matrix find if it matches the first character, if it matches then we have to look in 4 directions. If there is match in that direction proceed till we are end of the string. If match return true if not return false. We have to look in all the directions because the string can be in any of 4 directions. Also Math.abs takes care of wrap around (this was my big bug)

Working Java Code:

public class StringFinder {

    enum Direction {
        up, down, left, right
    };

    public static void main(String args[]) {
        char[][] ar = new char[][] { { 'a', 'e', 'r', 'o','p','s' },
                                     { 'b', 'h', 'a', 'r','l','s' },
                                     { 'w', 'r', 'i', 's','l','o' },
                                     { 'a', 's', 'n', 'k','t','q' },
                                     { 'a', 'e', 'r', 'o','p','s' },
                                     { 'b', 'h', 'a', 'r','l','s' },};
        String str = "rain";
        StringFinder sf = new StringFinder();
        System.out.print(sf.stringFinder(ar, str));
    }

    private boolean stringFinder(char[][] ar, String str) {
        int size = ar.length;
        if (str.length() > size + 1)
            return false;
        int k = 0;
        char[] charArray = str.toCharArray();
        for (int i = 0; i < size; i++)
            for (int j = 0; j < size; j++)
                if (ar[i][j] == charArray[k])
                    return isMatch(ar, charArray, i, Math.abs((j + 1) % size),
                            k + 1, Direction.right)
                            || isMatch(ar, charArray, Math.abs((i + 1) % size),
                                    j, k + 1, Direction.down)
                            || isMatch(ar, charArray, Math.abs((i - 1) % size),
                                    j, k + 1, Direction.up)
                            || isMatch(ar, charArray, i,
                                    Math.abs((j - 1) % size), k + 1,
                                    Direction.left);
        return false;
    }

    private boolean isMatch(char[][] ar, char[] charArray, int i, int j, int k,
            Direction dir) {
        int size = ar.length;
        if (k == charArray.length - 1) {
            if (ar[i][j] == charArray[k])
                return true;
            else
                return false;
        }
        if (ar[i][j] == charArray[k]) {
            if (dir == Direction.down)
                i = Math.abs((i + 1) % size);
            else if (dir == Direction.right)
                j = Math.abs((j + 1) % size);
            else if (dir == Direction.left)
                j = Math.abs((j - 1) % size);
            else
                // dir==Direction.up
                i = Math.abs((i - 1) % size);

            return isMatch(ar, charArray, i, j, k + 1, dir);
        }

        return false;
    }

}

Finding max and min

Q: Given an array of n elements, find the min and max in 3n/2 comparisons even in worst case.

We usually think of the following approach as soon as we see the question

One scan through the array with two extra variables to store current min and max.
In this approach the worst case number of comparisons = 2n

Can we change the approach slightly to make sure that even the worst case number of comparisons is 3*n/2

Following is the approach..

1) take 2 number at a time ....

2) compare these 2 numbers .... (1st comparison)

3) compare the minimum of these two with current minimum  (2nd comparison)

4) compare the max of these two with current max (3rd comparison)

as there are (n/2) pairs ... and 3 comparisons per a pair .... total comparisons are 3n/2 ....

No of occurrences of a number

Q: Given a sorted array find number of occurrences of a given number

If the interviewer has mentioned that the given array is in sorted array then he is expecting the solution to be in log( n ) time.

We can solve this using binary search. To find the no of occurrences of the given number we can find the first occurrence of the number and the last occurrence of the number and return the difference between them.

To find the first occurrence of a number we need to check for the following condition. Return the position if any of the following is true.

(mid == low && A[mid] == data) || (A[mid] == data && A[mid-1] < data)

To find the last occurrence of a number we need to check for the following condition. Return the position if any of the following is true.

(mid == high && A[mid] == data) || (A[mid] == data && A[mid+1] > data)

Working Java Code:

public class NoOfOccurences {

    public static int findFirstOccurence(int A[],int low,int high,int data)
    {
        int mid;
       
        while(low <= high)
        {
            mid = low + (high-low)/2;
            if(( mid == low && A[mid] == data) || (A[mid] == data && A[mid-1] < data))
            {
                return mid;
            }else if(A[mid] >= data)
            {
                high = mid-1;
            }else
            {
                low = mid+1;
            }   
        }
       
        return -1;
       
    }
   
    public static int findLastOccurence(int A[],int low,int high,int data)
    {
        int mid;
       
        while(low <= high)
        {
            mid = low + (high-low)/2;
            if(( mid == high && A[mid] == data) || (A[mid] == data && A[mid+1] > data))
            {
                return mid;
            }else if(A[mid] <= data)
            {
                low = mid+1;
            }else
            {
                high = mid-1;
            }   
        }
       
        return -1;
    }
    
    
    public static void main(String[] args) {
        int a[] = {1,2,3,3,3,3,4,5,6};
        int firstCount = NoOfOccurences.findFirstOccurence(a,0,8,3);
        int lastCount = NoOfOccurences.findLastOccurence(a,0,8,3);
       
        int noOfOccur = (lastCount - firstCount) +1;
        System.out.print("No of occurences"+noOfOccur);

    }

}

SubArray With sum zero.

Q: An array contain positive and negative elements, find maximum subarray whose sum is equal to zero.

Algorithm:

Lets take input array as a[]={-3,2,4,-6,-8,10,11}

Make an array b [] such that b[i]=b[i-1]+a[i]; means b[i] = sum(a[0],..., a[i]);

So b[]={-3,-1,3,-3,-11,-1,10}

Now all those pairs at indexes (i,j)in array b[] having equal numbers are the indexes of subarrays from (i+1,j) having sum as zero.

we have to find some (i, j) so: a[i] + a[i+1] + ... + a[j] = 0. But a[i] + a[i+1] + ... + a[j] = b[j] - b[i-1].
when creating the map using b values, the key in map is the value from b and the value in map is the index of from b. if a new key exists, this means we found a solution.

Finding all pairs in O(n) can be done by using map.

Working JAVA Code
---------------------------
import java.util.Comparator;
public class Index implements Comparable{
Integer start;
Integer end;
public Integer getStart() {
    return start;
}
public void setStart(Integer start) {
    this.start = start;
}
public Integer getEnd() {
    return end;
}
public void setEnd(Integer end) {
    this.end = end;
}
public int compareTo(Object index1) {
    index1 = (Index) index1;
    Index index2 = (Index) this;
    Integer  index1Distance = ((Index) index1).getEnd().intValue() -  ((Index) index1).getStart().intValue();
    Integer index2Distance = ((Index) index2).getEnd().intValue() -  ((Index) index2).getStart().intValue();
    if (index1Distance > index2Distance)
        return 1;
    else if (index1Distance == index2Distance)
        return 0;
    else
        return -1;
}
}

import java.util.HashMap;
import java.util.Map;
public class SubarraywithSumZero {
    public Index findLongestSubArraywithSumZero(long[] inputArray) {
        // 1. Generate a cummulative array
        for (int i=1; i < inputArray.length; i++) {
            inputArray[i] += inputArray[ (i-1)];
        }
        //2. Read the array, store it in map
        // For a subraary with 0 there should + and - numbers
        // we need to figure the longest distance indexes which have same numbers
        // since our array is cummulative postives and negatives which sum to 0 will bring the
        // intermittent array back to same number where it started
        // eg intermittent array = -6, -8, -10, -6, -4, 1, 2, 3, 4, 1
        // now from -6 we again reach -6
        // and later from 1 back to 1 which implies these two arrays are summing to 0
        // we just need the longest one
        Map<Integer, Integer> indexMap = new HashMap<Integer, Integer>();
        Index maxIndex = null;
        for (int i=0; i < inputArray.length; i++) {
            Integer index = new Integer(i);
            Integer val = new Integer((int) inputArray[i]);
            if (indexMap.get(val) == null) {
                indexMap.put(val, index);
            }
            else {
                if (maxIndex == null) {
                    maxIndex = new Index();
                    //collosion found the subarray
                    maxIndex.setStart(indexMap.get(val));
                    maxIndex.setEnd(new Integer(i));
                }
                else  {
                    Index index1 = new Index();
                    index1.setStart(indexMap.get(val));
                    index1.setEnd(new Integer(i));
                    if (maxIndex.compareTo(index1) <= 0) {
                        maxIndex = index1;
                    }
                }
            }
        }
            return maxIndex;       
    }
    public static void main(String[] args) {
        long inputArray[] = {3,2,4,-6,-8,10,11};
        SubarraywithSumZero subarraywithSumZero = new SubarraywithSumZero();
        Index maxIndex = subarraywithSumZero.findLongestSubArraywithSumZero(inputArray);
        System.out.println("Longgest Subarray with sum starts at [" + maxIndex.getStart() + " ] and ends at [" + maxIndex.getEnd() + "]");
    }
}