Serializing a binary tree

Q: Design an algorithm and write code to serialize and deserialize a binary tree.

Advantages of serialization/deserialization include storing a binary into and restoring it for a later point of time, transmitting the tree over a network from one computer and load it in another computer.

One approach for this problem could be the nodes with NULL values using some kind of sentinel so that later nodes can be inserted In correct place while deserialization. Lets use the sentinel as # and we will use preorder traversal here serialization.

Assume we have a binary tree below:

The preorder traversal of the above tree can be written as 

30 10 50 # # # 20 45 # # 35 # #

Finding Unique number

Q: You are given an array that contains integers. The integers content is such that every integer occurs 3 times in that array leaving one integer that appears only once.
Fastest way to find that single integer

eg:
Input: {1,1,1,3,3,3,20,4,4,4};

Answer: 20

The logic is similar to finding the element which appears once in an array - containing other elements each appearing twice. There we do XOR all the elements and the result will be the unique number.

To apply the similar logic to this problem we maintain 2 variables

ones - This variable holds XOR of all the elements which have appeared only once.
twos - This variable holds XOR of all the elements which have appeared twice.

The algorithm goes as follows…

1. A new number appears - It gets XOR' ed to the variable "ones".
2. A number gets repeated(appears twice) - It is removed from "ones" and XOR'd to the
variable "twos".
3. A number appears for the third time - It gets removed from both "ones" and "twos".

The final answer will be in "ones" as it holds the unique element.

Working Java code:

Multiplication of numbers

Q: There is an array A[N] of N numbers. You have to compose an array Output[N] such that Output[i] will be equal to multiplication of all the elements of A[N] except A[i]. For example Output[0] will be multiplication of A[1] to A[N-1] and Output[1] will be multiplication of A[0] and from A[2] to A[N-1]. Solve it without division operator and in O(n).

A: {4, 3, 2, 1, 2}
OUTPUT: {12, 16, 24, 48, 24}

Since we should not use, division operator, Brute force approach would be O(n^2)

Other approach is by storing the result temporarily in an array.

Let’s define array B where element B[i] = multiplication of numbers from A[0] to A[i]. For example, if A = {4, 3, 2, 1, 2}, then B = {4, 12, 24, 24, 48}. Then, we scan the array A from right to left, and have a temporary variable called product which stores the multiplication from right to left so far. Calculating OUTPUT[i] is straight forward, as OUTPUT[i] = B[i-1] * product.

Above approach requires O( n ) time and also O( n ) space.

We can actually avoid the temporary array. We can have two variables called left and right, each keeping track of the product of numbers multiplied from left->right and right->left.

Robot Unique Paths

Q: A robot is located at the top-left corner of a m x n grid. The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid. How many possible unique paths are there?

We can solve this problem using backtracking approach.

Other approach is using dynamic programming with memorization.

Longest Palindrome in a string

Brute force Algorithm.

1. Have 2 for loops
   for i = 1 to i less than array.length -1
   for j=i+1 to j less than array.length
2. This way you can get substring of every possible combination from the array
3. Have a palindrome function which checks if a string is palindrome
4. so for every substring (i,j) call this function, if it is a palindrome store it in a string variable
5. If you find next palindrome substring and if it is greater than the current one, replace it with current one.
6. Finally your string variable will have the answer

Brute force approach for this problem takes O(n3) time.

Another approach is

1. Reverse the string and store it in different string
2. Now find the largest matching substring between both the strings

This too will take O(n2) time

We can solve this problem using suffix trees, but constructing the suffix tree itself seems to be more complex in terms of both time and space complexity.

We can solve this problem using a better approach which will revolve around with a center for every single character.

For each position in the string we store an upper and lower pointer that tracks the upper and lower bounds of the largest palindrome centered at that position.

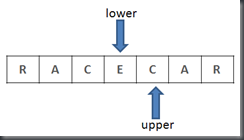
For instance, position 2 in the string "racecar" would start as:

At this point, the longest known palindrome at position 2 is the single character 'c'. We then increment the upper pointer and decrement the lower pointer and compare their respective values.

Since the upper and lower values are not the same, we stop and now know that the longest palindrome centered at position 2 is 'c'. We then start the process again at the next string position, 3.

We increment and decrement the upper and lower pointers and see that they are equal. Our current longest palindrome centered at position 3 is now 'cec'.

Since they were equal, we increment and decrement the pointers again and see that they are still equal. Our new longest palindrome centered at position 3 is now 'aceca'.

We continue incrementing and decrementing the upper and lower pointers until they don't match or they hit one of the ends of the string.

Since our pointers are equal, we increment and decrement them again. We hit an end of the string and the pointers are equal so we know that our longest palindrome centered at position 3 is 'racecar'.

We're done with position 3 and continue this same process again at position 4. We'll do this until we've covered every position in the string.

NOTE: We initially assumed that the palindrome had an odd length. This algorithm works for even palindromes as well. The only change we make is that when we initialize the pointers, instead of having the lower and upper pointer point to the same position we have the upper pointer point at the next position. Everything else with the algorithm remains the same. i.e. The initial pointers for an even palindrome 'centered' at position 3 would look like:

Runtime:

Worst-Case: O(N^2)

Best-Case: O(N)

The worst case is achieved when the string is a single repeated character because every substring is a palindrome.

The best case is achieved when the string contains no palindromes.

Typically if a string only contains a single palindrome (the fewer the better), the closer to O(N) it will run. This is because every time it checks a position in the string, it checks the character before and after that position, and if they don't match then it stops looking for the palindrome. Positions in the string can be discarded after only one lookup if that position doesn't have a palindrome, so if there are no palindromes you only do N comparisons.

JavaCode:

3 sum and 2 sum problem

Q: Given an integer x and an unsorted array of integers, describe an algorithm to determine whether two of the numbers add up to x.

If we have hash table, we can just check for every number ‘a’, if x-‘b’ is present in hash table. This takes O( n ) with constant space for hashtable. What if the interviewer hates the hashtable.

Sort the array. Then, keep track of two pointers in the array, one at the beginning and one at the end. Whenever the sum of the current two integers is less than x, move the first pointer forwards, and whenever the sum is greater than x, move the second pointer backwards. This solution takes O(n log n) time because we sort the numbers.

Another approach for this problem could be…

Create a binary search tree containing x minus each element in the array. Then, check whether any element of the array appears in the BST. It takes O(n log n) time to create a binary search tree from an array, since it takes O(log n) time to insert something into a BST, and it takes O(n log n) time to see if any element in an array is in a BST, since the lookup time for each element in the array takes O(log n). Therefore step one takes O(n log n) time and step two takes O(n log n) time, so our total running time is O(n log n).

Variations for this problem would be, find three integers a,b,c in the array such that a+b=c

This will  take O(n²) time complexity.

Other variation is Find three integers a,b,c in the array such that a+b+c =0

Median of two sorted arrays

This question is similar to the previous question which can solved in O(logn) using binary search approach. Lets see the algorithm….

Algorithm
1.Let the two arrays be a1,a2 with n elements each with n elements
2.Let med1 and med 2 be the medians of two arrays respcetively
3.if med1==med2 means the required median is med1(or med2)
4.if med1 < med2 that means the median can either lie in upper half of a1 or lower half  of a2     5.if med1 >med2 that means the median can be in lower half of of a1 or upper half of a2
we continue this process until two elements are present in the array
if two elements are present in the array then we calculate the median as follows
median_required = (max(a1[0],a2[0])+min(a1[1]+a2[1])) /2

Kth Smallest element

Q: Given two sorted arrays A, B of size m and n respectively. Find the k-th smallest element in the union of A and B. You can assume that there are no duplicate elements.

One approach we could think of is merge both arrays and the k-th smallest element could be accessed directly. Merging would require extra space of O(m+n). The linear run time is pretty good, but could we improve it even further?

Another approach is using two pointers, you can traverse both arrays without actually merging them, thus without the extra space. Both pointers are initialized to point to head of A and B respectively, and the pointer that has the larger of the two is incremented one step. The k-th smallest is obtained by traversing a total of k steps.

We can solve this problem in logarithmic time in O(lg m + lg n) using binary search approach.

We try to approach this tricky problem by comparing middle elements of A and B, which we identify as A_i and B_j. If A_i is between B_j and B_j-1, we have just found the i+j+1 smallest element. Therefore, if we choose i and j such that i+j = k-1, we are able to find the k-th smallest element. This is an important invariant that we must maintain for the correctness of this algorithm.

Maintaining the invariant
    i + j = k – 1,

If B_j-1 < A_i < B_j, then A_i must be the k-th smallest,
or else if A_i-1 < B_j < A_i, then B_j must be the k-th smallest.

We can make an observation that when A_i < B_j, then it must be true that A_i < B_j-1. On the other hand, if B_j < A_i, then B_j < A_i-1.

Using the above relationship, it becomes clear that when A_i < B_j, A_i and its lower portion could never be the k-th smallest element. So do B_j and its upper portion. Therefore, we could conveniently discard A_i with its lower portion and B_j with its upper portion.

Saving a Binary Search Tree to a File

Q: Describe an algorithm to save a Binary Search Tree (BST) to a file in terms of run-time and disk space complexity. You must be able to restore to the exact original BST using the saved format

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be “resurrected” later in the same or another computer environment.

Pre-order traversal is the perfect algorithm for making a copy of a BST. We can store the preorder traversal of the tree into File and then read it again to construct the tree. Assuming we have a file where the pre order traversal of the tree is written to it, We will now see how to read the file to construct that into BST.

Sorted List to Balanced Binary Search Tree

Q: Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

We can solve this problem using bottom up approach with recursion. We create nodes bottom-up, and assign them to its parents. The bottom-up approach enables us to access the list in its order while creating nodes.  Lets define the node structure for Binary Search Tree Node as follows

Below is the java code for converting a singly linked list to a balanced BST. The algorithm requires the list’s length to be passed in as the function’s parameters. The list’s length could be found in O(N) time by traversing the entire list’s once. The recursive calls traverse the list and create tree’s nodes by the list’s order, which also takes O(N) time. Therefore, the overall run time complexity is still O(N).

Word Suggest

This is general algorithm we use in search engines. Question is Given a dictionary suggest the words for a given misspelled word.

The word could be misspelled in either of the following 4 ways.

1. Transpositions: These are set of words where 2 adjacent characters in a word are trans positioned. Ex: hlelo –> hello . There are atmost n-1 trans positioned words for a given word.
2. Insertion: Word could be misspelled by inserting an extra character. Ex: helxlo –> hello There could be at the max n+1 words with this.
3. Substitution: Word could be misspelled by typing wrong character in place of another character. Ex: helxo –> hello . Max No. of Substituted words could 25 * ( n )
4. Omissions: These are set of words where a character is omitted Ex: hllo –> hello . Max No of omitted words could be 26*(n+1)

Lets code them now.

Suffix Trees

Suffix Tree for a String T is Trie like data that represents the suffixes of T. For example, if your word were bibs, you would create the following tree.

Suffix trees answers the queries related to one string. There are many applications of suffix trees. Some of them are..

1. String Matching and Pattern Matching algorithm
2. Longest Repeated SubString
3. Longest palindrome
4. Longest common substring
5. Longest Common prefix

Sample java Implementation of Suffix Tree:

String Search

Searching for a substring, pat[1..m], in txt[1..n], can be solved in O(m) time (after the suffix tree for txt has been built in O(n) time).

Longest Repeated Substring

Add a special ``end of string'' character, e.g. `$', to txt[1..n] and build a suffix tree; the longest repeated substring of txt[1..n] is indicated by the deepest fork node in the suffix tree, where depth is measured by the number of characters traversed from the root, i.e., `issi' in the case of `mississippi'. The longest repeated substring can be found in O(n) time using a suffix tree.

Longest Common Substring

The longest common substring of two strings, T1 and T2, can be found by building a generalized suffix tree for T1  and T2 : Each node is marked to indicate if it represents a suffix of T1 or T2 or both. The deepest node marked for both T1 and T2 represents the longest common substring.

Equivalently, one can build a (basic) suffix tree for the string T1$T2#, where `$' is a special terminator for T1 and `#' is a special terminator for T2. The longest common substring is indicated by the deepest fork node that has both `...$...' and `...#...' (no $) beneath it.

Palindromes

A palindrome is a string, P, such that P=reverse(P). e.g. `abba'=reverse(`abba'). e.g. `ississi' is the longest palindrome in `mississippi'.

The longest palindrome of T can be found in O(n) time, e.g. by building the suffix tree for T$reverse(T)# or by building the generalized suffix tree for T and reverse(T).

Linked List Question

Q: Given a linked list with two pointers in node structure where one points to the next node and the other pointer points to some random node in the linked list. Write a program to create a copy of this linked list

The above problem can be solved in O( n ) time and in constant space complexity. Assuming the Node Structure as following..

Algorithm:

1)[Merge listst]Create list B this way: for each NodeA in A create a NodeB in B , copy NEXT ptr to NodeB: NodeB{NEXT} = NodeA{NEXT} and change NEXT ptr in NodeA to this newly created node in B: NodeA{NEXT}=NodeB;
2) go through the list A (NB: you have to jump through the nodes of B!) and set NEXTRND ptr in next B nodes to the next ptrs after next_random nodes: NodeA{NEXT}{NEXTRND}=NodeA{NEXTRNF}{NEXT};
After that all NEXTRND nodes in list B will be pointing to correct nodes in B;
3) [Un-merge]. For each node in A and in NEXT node B set correct NEXT ptrs:
node=headA;
while(node){tmp = node{NEXT}; node{NEXT}=tmp?tmp{NEXT}:NULL; node=tmp;}
After this process all {NEXT} nodes in both lists A and B will be correct

Java Code:

Best days to sell and buy stock, if array of stock prices given

Q: Say you have an array for which the ith element is the price of a given stock on day i. If you were only permitted to buy one share of the stock and sell one share of the stock, design an algorithm to find the best times to buy and sell

Algorithm: Go through the array in order, keeping track of the lowest stock price and the best deal you've seen so far. Whenever the current stock price minus the current lowest stock price is better than the current best deal, update the best deal to this new value.

Working Java Code:

Arranging elements in specific order

n a given array of elements like [a1, a2, a3, a4, ..... an, b1, b2, b3, b4, ....... bn, c1, c2, c3, c4, ........ cn] without taking a extra memory how to merge like [a1, b1, c1, a2, b2, c2, a3, b3, c3, ............ an, bn, cn]

Triplet (x,y,z) whose distance is min

Given 3 sorted arrays (in ascending order). Let the arrays be A(of n1 length), B(of n2 length), C(of n3 length). Let x be an element of A, y of B, z of C. The distance between x, y and z is defined as the max(|x-y|,|y-z|,|z-x|). Find the tuple with the minimum distance?

Working java Code:

Selecting k smallest or largest elements

There are cases when you need to select a number of best (according to some definition) elements out of finite sequence (list). For example, select 10 most popular baby names in a particular year or select 10 biggest files on your hard drive.  

While selecting single minimum or maximum element can easily be done iteratively in O(n) selecting k smallest or largest elements (k smallest for short) is not that simple. One approach could be sort the elements and take the first k elements. But that requires O( nlogn) time.

Priority Queue can be used for better performance if only subset of sorted sequence is required. It requires O(n) to build priority queue based on binary min heap and O(k log n) to retrieve first k elements. Can we improve this further?

Quicksort algorithm picks pivot element, reorders elements such that the ones less than pivot go before it while greater elements go after it (equal can go either way). After that pivot is in its final position. Then both partitions are sorted recursively making whole sequence sorted. In order to prevent worst case scenario pivot selection can be randomized.

Basically we are interested in the k smallest elements themselves and not the ordering relation between them. Assuming partitioning just completed let’s denote set of elements that are before pivot (including pivot itself) by L and set of elements that are after pivot by H. According to partition definition L contains |L| (where |X| denotes number of elements in a set X) smallest elements. If |L| is equal to k we are done. If it is less than k than look for k smallest elements in L. Otherwise as we already have |L| smallest elements look for k - |L| smallest elements in H.

Working Java Code:

Queue based on single stack

Queue based on 2 stacks is generally what we usually know of and probably would be on our minds while answering such questions. We could solve the same using one stack and taking advantage of recursion. We will see how we can solve this with no additional storage.

Assume that items come out of stack in the order they must appear in the queue (FIFO). Choosing the opposite order is also possible however is not practical. To make it happen we simply need to make sure that items in the stack (LIFO) are placed in the opposite order. Items queued first must appear at the top of the stack. This basically means that in order to queue item all items must be popped, the item  pushed and then existent items pushed inversely to pop order. But we have no additional explicit storage requirement. Then store items implicitly through recursion.

Enqueue is a O(n) operation (where n is the number items in the stack). Dequeue and Peek is a O(1) operation.

Cumulative sum of a tree at each node.

Q: Given a binary tree, print the sum( inclusive of the root ) of sub-tree rooted at each node in in-order

This question can be answered in two ways. We can do it using two passes with constant space of with one pass and O( n ) space.

Lets say the tree node is as follows

Converting a Tree to a double Linked List

Q: Write a program which will accept Binary Search Tree and convert it to a sorted Double Linked List.

For example if the Binary search tree is as shown below…

Then the converted doubly linked  list should be

Lets define the Node structure of the tree as follows

We can use recursive approach to solve this by just arranging the pointers..

Algorithm:

If tree is not empty

Convert Left Subtree to List and let hLeft point to it

Convert Right Subtree to List and left hRight point to it.

Append hLeft to root and then hRight

Working java Code: