Next largest palindrome

Q: A number is given as a palindrome, write a function to return the next largest palindrome.

Algorithm:

Case I: The given number is a palindrome..ex: 1234321 then simply increment the centre digit by 1 i.e the answer is 1235321

Case II: The given number is not a palindrome:

Subcase 1: The number to the left of the middle digit is greater than the number on the right ex:2194135 (here 219 > 135) then,reverse the left side numbers and replace the right side numbers with them, therefore the answer will be 2194912.

Subcase 2:The number to the right of the middle digit is greater than the number on the left ex:1354219 then,
then increment the middle digit by 1 and then reverse the left side numbers and replace the right side numbers with them. Therefore the answer would be 135 5(middle digit incremented) 531(reversed), resulting in 1355531, which is the next palindrome.
Note: in case the middle digit is 9 then incrementing it would make it 10, so put 0 instead of 9 and increment the first right and left neighbouring digit of 9 by 1.

Subsets that match a given sum in an array

Q: Find subsets that match a given sum in an array

Common Element in a binary search tree

Q: Given two BST's A, B, Find All elements of A which are present in B

OR

You are given the root nodes of two BST and you have to print the common elements in them.

Max loss of the stock

Given an array of stock prices from day 0 to N-1 of a company X, we have to find the max loss that is possible. Loss occurs if stock is bought at higher price and sold at lower price.
Ex: 1 2 3 7 5 8 9 4 6 10 12
Max Loss is 9 - 4 = 5 (Possible losses are 8-4 = 4, 7-5 = 2 etc). Max difference between stock price is 12 - 1 = 11 but max loss is 9 -4 = 5

Code:

Pythogorous triplets

Q: How to find pythagorean triplets in an array?

OR

Q: Given an array, find all such triplets i,j and k, such that a[i]² = a[j]²+a[k]²

Pythagorean triplet is a set {a,b,c} such that a² = b² + c². Example: for array [9, 2, 3, 4, 8, 5, 6, 10] the output of the algorithm should be {3, 4, 5} and {6, 8, 10}

Algorithm:

Square each element. (This takes O(n) time). This will reduce the original task to "find three numbers in array, one of which is the sum of other two".

1. Sort the array in ascending order. This takes O(n log n).
2. Now consider each element a[i]. If a[i]=a[j]+a[k], then, since numbers are positive and array is now sorted, k<i and j<i. To find such indexes, run a loop that increases j from 1 to i, and decreases k from i to 0 at the same time, until they meet. Increase j if a[j]+a[k] < a[i], and decrease k if the sum is greater than a[i]. If the sum is equal, that's one of the answers, print it, and shift both indexes. This takes O(i) operations.
   
3. Repeat step 2 for each index i. This way you'll need totally O(n²) operations, which will be the final estimate.

Code:

Time Complexity : Efficiency is (i) O(nlogn) : for sorting (ii) O(n^2) : for finding pairs adding equal to A[i] So total efficeincy is O(n^2)

Merging sorted 1st half and 2nd half

Q: Given an integer array of which both first half and second half are sorted. Write a function to merge the two parts to create one single sorted array in place [do not use any extra space]. e.g. If input array is [1,3,6,8,-5,-2,3,8] It should be converted to: [-5,-2,1,3,3,6,8,8]

The idea is to Insert all elements of second half into first half., like we do in Insertion Sort.

we need to keep the arrays sorted while we doing the swaps

Design a web crawler

Web crawler is a program that traverses the hyperlinks structure of web pages. We crawler visits each web page by following the hyperlinks on previous page it visits. while it is crawling web pages to extract hyperlinks, a web crawler also save each page it has visited.

Crawler basic algorithm

1. Remove a URL from the unvisited URL list
2. Determine the IP Address of its host name
3. Download the corresponding document
4. Extract any links contained in it.
5. If the URL is new, add it to the list of unvisited URLs
6. Process the downloaded document
7. Back to step 1

Single Crawler

Multithreaded Crawler

Parallel Crawler

Search Engine : architecture

Search Engine : major components

• Crawlers
  Collects documents by recursively fetching links from a set of starting pages.Each crawler has different policies The pages indexed by various search engines are different
• The Indexer
  Processes pages, decide which of them to index, build various data structures representing the pages (inverted index,web graph, etc), different representation among search engines. Might also build additional structure ( LSI )
• The Query Processor
  Processes user queries and returns matching answers in an order determined by a ranking algorithm

Issues on crawler

• General architecture
• What pages should the crawler download ?
• How should the crawler refresh pages ?
• How should the load on the visited web sites be minimized ?
• How should the crawling process be parallelized ?

Distributed crawler

The crawler system should consist of a number of crawler entities, which run on distributed sites and interact in peer-to-peer fashion. Each crawler entity has to have the knowledge to its URL subset, as well as mapping from URL subset to network address of corresponding peer crawler entity.

Whenever the crawler entity encounters a URL from a different URL subset, it should forward to the appropriate peer crawler entity based on URL subset to crawler entity lookup.

Each crawler entity should maintain its own database, which only stores the URL’s from the URL subset assigned to the particular entity. The databases are disjoint and can be combined offline when the crawling task is complete.

Crawler Entity Architecture

Each crawler entity consists of a number of crawler threads, a URL handling thread, a URL packet dispatcher thread and URL packet receiver thread. The URL set assigned to each crawler entity will be further divided into subsets for each crawler thread.

Each crawler thread should have its own pending URL list, a DNS cache. Each thread picks up an element from URL pending list, check to see if the IP corresponding to URL is available in the DNS cache, else does a DNS lookup, generates a HTTP fetch requests, gets the page and finally extracts more URL’s from the fetched page and puts them in the job pending queue of the URL handling thread.

URL handling thread will have a job queue. It will get a URL from the job queue, checks to see if the URL belongs to the URL set corresponding to the crawler entity, if it belongs to another entity it will put the URL on the dispatcher queue and get a new URL from the its job queue. If the URL belongs to its set, it firsts checks the URL-seen cache, if the test fails it queries the SQL database to check if the URL has been seen, and puts the URL in the URL-seen cache. It then puts the URL into URL pending list of one of the crawler threads. URLs are assigned to a crawler thread based on domain names. Each domain name will only be serviced by one thread; hence only one connection will be maintained with any given server. This will make sure that the crawler doesn’t overload a slow server.

URL dispatcher thread will communicate the URL’s corresponding crawler entity.

A URL receiver thread collects the URL’s received from other crawler entities i.e. communicated via dispatcher threads of those crawler entities and puts them on the job queue of the URL handling thread.

Buffer Overflow

Question: What is a buffer overflow and how do you exploit it?

What is Buffer Overrun?

Buffer Over-run refers to problem where we can make program to use more than allotted ‘buffer’.All buffer overruns cannot be exploited as security vulnerability

What it could lead to?

Buffer overflows can be triggered by inputs that are designed to execute code, or alter the way the program operates. You get an access violation (AV). Your site becomes unstable.The attacker injects code into your application, executes it, and makes everyone an administrator of your site.

Types of Buffer Overrun

• Stack Overruns
• Heap Overruns
• Array Indexing Errors
• Format String
• Unicode and ANSI Buffer size mismatch

A colleague of mine created a  PPT on Buffer Overflow which we deal with here on daily basis. I removed some of the proprietary code and some other useful information.

Buffer OverFlow

View more presentations from Rambabu Duddukuri.

Max Black sub square matrix

Imaging there is a square matrix with n x n cells. Each cell is either filled with a black pixel or a white pixel. Design an algorithm to find the maximum subsquare such that all four borders are filled with black pixels.

Algorithm to Exhibit Did You Mean Feature of Google Search Engine

When people search at Google, they often type two words without space. For example, instead of typing "binary tree", someone can type "binarytree". Given an input, what is a good way of finding if it is a combination of two valid words e.g. In Directly You have Add Space between two such or if are using some data structure , where words would have been inserted , you would have maintained a boolean variable to defined the end of word (eod)
An Example Will be Let's say you have a phrase without any spaces - eg. "thisisawesome". Given a dictionary, how would you add spaces in this string?

You can solve this problem using a trie datastructure. Trie data structure implementation can be found here in my previous blog. The rest is just searching the trie

LRU Cache Implementation

Linked List is a palindrome or not

Question: Write a program to check if the given linked list is a palindrome or not

METHOD 1 (using recursion)

METHOD 2 (Using Stack)

• Get the middle of the linked list.
  
  
• Push the elements into the stack till the middle of the linked list
  
  
• Compare the top of the stack and second half.
  

Next bigger number

Q : You have given a positive number. You have to find a number which is immediate bigger than that by using same digits available in the number. use same digits with same number of time, coming in positive integer and if a small number is not possible then we have to return -1.

For example: (1) You have given a number 7585 , your output should be 7855 . (2) 7111, return –1

Algorithm:

Code:

Building Bridges:

Problem: Consider a 2-D map with a horizontal river passing through its center. There are n cities on the southern bank with x-coordinates a1….an and n cities on the northern bank with x coordinates b1….bn. The cities on each bank are also numbered 1 through n and these numbers do not correspond to the ordering of the x-coordinates. You can only build a bridge from a city on the south bank to a city on the north bank with the same number. No two bridges may cross each other. An example of a valid bridge building is shown in Figure 1. Give an algorithm for finding the maximum number of bridges that can be built.

Solution:
Consider the sequences A = N(a1),……..,N(an) and B = N(b1),…….,N(bn) where N(ai) is the number of the city with x-coordinate ai. The length of the longest common subsequence of A and B is the maximum number of bridges. Since A and B are non-repeating, the length of the LCS for A and B can be calculated in O(n log n) time. Make sure you understand why that is the case!

Proof that length of the LCS is the maximum number of bridges: We show that the maximum number of bridges cannot be more than the length of the LCS and that the maximum number of bridges cannot be less than the length of the LCS.
Firstly, assume the length of the LCS is m. Let c1,…….,cm be a longest common subsequence of A and B, corresponding to cities ai₁……ai_m in A and bj₁,,,,,,,, bj_m in B. Then for 0 < k< = m, we can draw a bridge from ai_k to bi_k . None of these bridges intersect. Therefore, we can draw at least as many bridges as the length of the LCS.

Now assume we can draw at most m bridges from cities CA = ai₁,…..ai_m to cities CB = bj₁,….., bj_m and WLOG assume CA is ordered by increasing x-coordinate. Then N(ai_k ) = N(bj_k ) since we can draw a bridge between them. Moreover, bj_k must have a higher x-coordinate than any of bj₁,…..bj_k-1 and a lower x-coordinate than any of bj_k+1,…..,bj_m so that none of the bridges cross.Therefore CA is a subsequence of A and CB is a subsequence of B and we have found a common subsequence. Thus, the length of the LCS is at least the maximum number of bridges

Edit Distance

Problem: Given two text strings A = a1a2….an of length n and B = b1b2…bm of length m, you want to transform A into B with a minimum number of operations of the following types: delete a character from A, insert a character into A, or change some character in A into a new character. The minimal number of such operations required to transform A into B is called the edit distance between A and B. Give an algorithm for finding the edit distance from A to B.

Solution:
Recursion Relation: We recurse on m(i; j), the minimum number of operations to change A(1 : i) into B(1 : j). The relation is

Running Time: m has nm elements and evaluating each element takes O(1) time for a total running time of O(nm).

Balanced Partitions:

Suppose you are given an array of n integers {a1,……, an} between 0 and M. Give an algorithm for dividing these integers into two sets x and y such that the difference of the sum of the integers in each set, is minimized.

For example, given the set {2,3,2,7,9}, you can divide it into {2, 2, 7} (sums to 11) and {3; 9} (sums to 12) for a difference of 1.

Solution:
Recursion Relation: Consider just the set of the numbers {a1,…..,aj}. What sums can we make with that set or subsets of it? We can make

• Any sums we could make with a subset of {a1,….,aj-1}
• Any sums we could make with a subset of {a1,….,aj-1} + aj

So: Let C_ij be 1 if a subset of {a1,…..,ai} adds to j and 0 otherwise. The recursion relation for C_ij is

We find the value of j, let it be b, closest to

such that C_nj = 1. The minimum difference is 2(T - b).
Running Time: We need only let j go to nM since the integers are bounded. Therefore, the size of C is n²M and filling it in takes O(1) per entry for a total running time of O(n²M).

A dynamic programming solution to this problem is provided in this video tutorial by Brian C. Dean. It is problem number 7.

Algorithm:
Firstly this algorithm can be viewed as knapsack problem where individual array elements are the weights and half the sum as total weight of the knapsack.

1.take a solution array as boolean array sol[] of size sum/2+1

2. For each array element,traverse the array and set sol [j] to be true if sol [j - value of array] is true

3.Let halfsumcloser be the closest reachable number to half the sum and partition are sum-halfsumcloser and halfsumcloser.

4.start from halfsum and decrease halfsumcloser once everytime until you find that sol[halfsumcloser] is true

Box Stacking

Problem:  You are given a set of boxes {b1,……,bn}. Each box bj has an associated width wj , height hj and depth dj . Give an algorithm for creating the highest possible stack of boxes with the constraint that if box bj is stacked on box bi, the 2D base of bi must be larger in both dimensions than the base of bj . You can of course, rotate the boxes to decide which face is the base, but you can use each box only once.
For example, given two boxes with h1 = 5;w1 = 5; d1 = 1 and h2 = 4;w2 = 5; h2 = 2, you should orient box 1 so that it has a base of 5x5 and a height of 1 and stack box 2 on top of it oriented so that it has a height of 5 for a total stack height of 6.

Solution:

Recursion: Memorize over H(j,R), the tallest stack of boxes with j on top with rotation R.

Running Time: The size of H is O(n |R_j|) where R is the number of possible rotations for a box.For our purposes, |R| = 3 (since we only care about which dimension we designate as the \height") so |H| = O(n). Filling in each element of H is also O(n) for a total running time of O(n²).

Code:

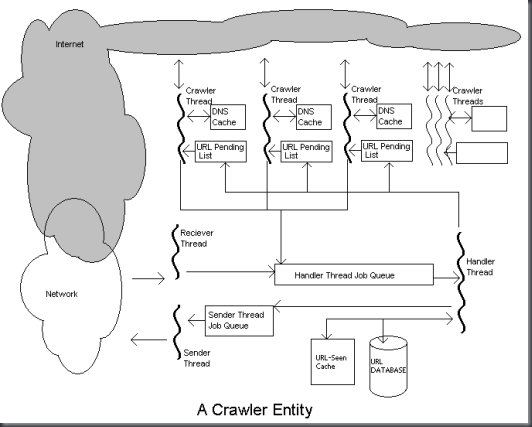
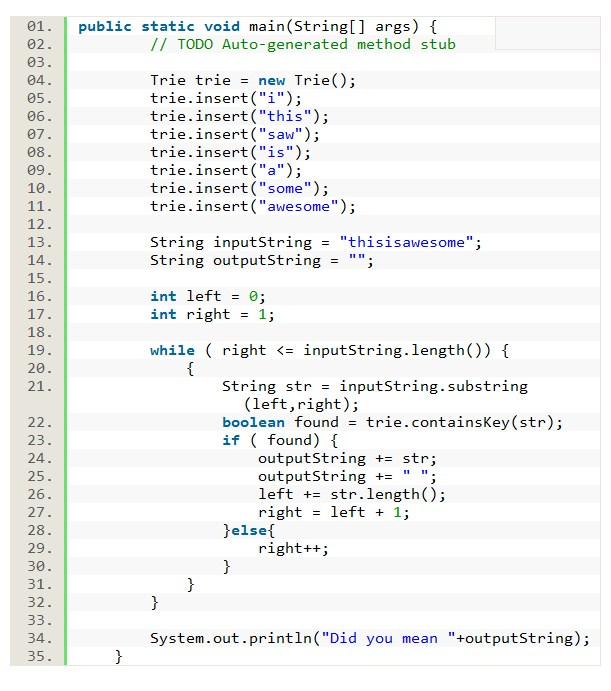
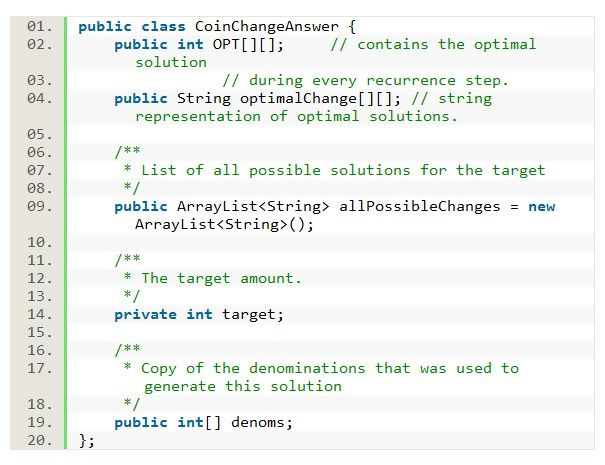
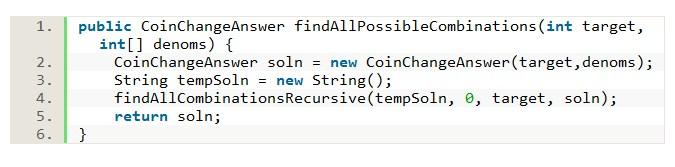
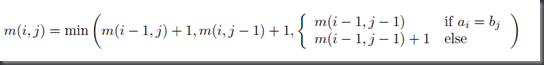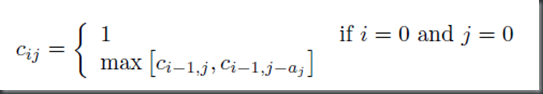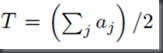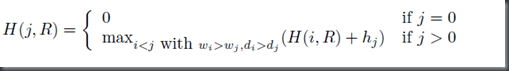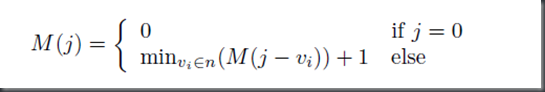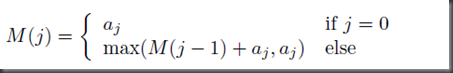   1: public static int stackHeight(ArrayList<Box> boxes) {
   2:         if (boxes == null) {
   3:             return 0;
   4:         }
   5:         int h = 0;
   6:         for (Box b : boxes) {
   7:             h += b.height;
   8:         }
   9:         return h;
  10:     }
  11:     
  12:     public static ArrayList<Box> createStackR(Box[] boxes, Box bottom) {
  13:         int max_height = 0;
  14:         ArrayList<Box> max_stack = null;
  15:         for (int i = 0; i < boxes.length; i++) {
  16:             if (boxes[i].canBeAbove(bottom)) {
  17:                 ArrayList<Box> new_stack = createStackR(boxes, boxes[i]);
  18:                 int new_height = stackHeight(new_stack);
  19:                 if (new_height > max_height) {
  20:                     max_stack = new_stack;
  21:                     max_height = new_height;
  22:                 }
  23:             }
  24:         }
  25:         
  26:         if (max_stack == null) {
  27:             max_stack = new ArrayList<Box>();
  28:         }
  29:         if (bottom != null) {
  30:             max_stack.add(0, bottom);
  31:         }
  32:         
  33:         return max_stack;
  34:     }
  35:     
  36:     public static ArrayList<Box> createStackDP(Box[] boxes, Box bottom, HashMap<Box, ArrayList<Box>> stack_map) {
  37:         if (bottom != null && stack_map.containsKey(bottom)) {
  38:             return stack_map.get(bottom);
  39:         }
  40:         
  41:         int max_height = 0;
  42:         ArrayList<Box> max_stack = null;
  43:         for (int i = 0; i < boxes.length; i++) {
  44:             if (boxes[i].canBeAbove(bottom)) {
  45:                 ArrayList<Box> new_stack = createStackDP(boxes, boxes[i], stack_map);
  46:                 int new_height = stackHeight(new_stack);
  47:                 if (new_height > max_height) {
  48:                     max_stack = new_stack;
  49:                     max_height = new_height;
  50:                 }
  51:             }
  52:         }        
  53:         
  54:         if (max_stack == null) {
  55:             max_stack = new ArrayList<Box>();
  56:         }
  57:         if (bottom != null) {
  58:             max_stack.add(0, bottom);
  59:         }
  60:         stack_map.put(bottom, max_stack);
  61:         
  62:         return (ArrayList<Box>)max_stack.clone();
  63:     }
  64:         
  65:     
  66:     public static void main(String[] args) {
  67:         Box[] boxes = { new Box(1, 7, 4), new Box(2, 6, 9), new Box(4, 9, 6), new Box(10, 12, 8),
  68:                         new Box(6, 2, 5), new Box(3, 8, 5), new Box(5, 7, 7), new Box(2, 10, 16), new Box(12, 15, 9)};
  69:  
  70:         //ArrayList<Box> stack = createStackDP(boxes, null, new HashMap<Box, ArrayList<Box>>());
  71:         ArrayList<Box> stack = createStackR(boxes, null);        
  72:         for (int i = stack.size() - 1; i >= 0; i--) {
  73:             Box b = stack.get(i);
  74:             System.out.println(b.toString());
  75:         }
  76:     }
  77:  
  78: public class Box {
  79:     public int width;
  80:     public int height;
  81:     public int depth;
  82:     public Box(int w, int h, int d) {
  83:         width = w;
  84:         height = h;
  85:         depth = d;
  86:     }
  87:     
  88:     public boolean canBeUnder(Box b) {
  89:         if (width > b.width && height > b.height && depth > b.depth) {
  90:             return true;
  91:         }
  92:         return false;
  93:     }
  94:     
  95:     public boolean canBeAbove(Box b) {
  96:         if (b == null) {
  97:             return true;
  98:         }
  99:         if (width < b.width && height < b.height && depth < b.depth) {
 100:             return true;
 101:         }
 102:         return false;        
 103:     }
 104:     
 105:     public String toString() {
 106:         return "Box(" + width + "," + height + "," + depth + ")";
 107:     }
 108: }

Making change : Coin denomination problem

Problem: You are given n types of coins with values {v1,…..,vn} and a cost C. You may assume v1 = 1 so that it is always possible to make any cost. Give an algorithm for finding the smallest number of coins required to sum to C exactly.
For example, assume you coins of values 1, 5, and 10. Then the smallest number of coins to make 26 is 4: 2 coins of value 10, 1 coin of value 5, and 1 coin of value 1.

Solution:

Recursion: We recurse on M(j), the minimum number of coins required to make change for cost j.

Running Time: M has C elements and computing each element takes O(n) time so the total running time is O(nC).

Working code:

All Possible Solutions

Optimal Solution

The optimal solution to this program can be found by using dynamic programming and its runtime can be considerably reduced by a technique called memoization.