Balanced Partitions:

Suppose you are given an array of n integers {a1,……, an} between 0 and M. Give an algorithm for dividing these integers into two sets x and y such that the difference of the sum of the integers in each set, is minimized.

For example, given the set {2,3,2,7,9}, you can divide it into {2, 2, 7} (sums to 11) and {3; 9} (sums to 12) for a difference of 1.

Solution:
Recursion Relation: Consider just the set of the numbers {a1,…..,aj}. What sums can we make with that set or subsets of it? We can make

• Any sums we could make with a subset of {a1,….,aj-1}
• Any sums we could make with a subset of {a1,….,aj-1} + aj

So: Let C_ij be 1 if a subset of {a1,…..,ai} adds to j and 0 otherwise. The recursion relation for C_ij is

We find the value of j, let it be b, closest to

such that C_nj = 1. The minimum difference is 2(T - b).
Running Time: We need only let j go to nM since the integers are bounded. Therefore, the size of C is n²M and filling it in takes O(1) per entry for a total running time of O(n²M).

A dynamic programming solution to this problem is provided in this video tutorial by Brian C. Dean. It is problem number 7.

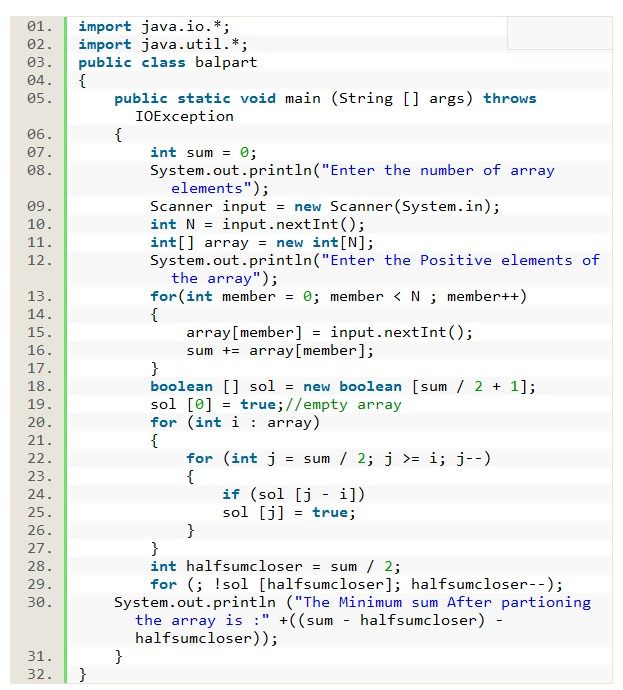
Algorithm:
Firstly this algorithm can be viewed as knapsack problem where individual array elements are the weights and half the sum as total weight of the knapsack.

1.take a solution array as boolean array sol[] of size sum/2+1

2. For each array element,traverse the array and set sol [j] to be true if sol [j - value of array] is true

3.Let halfsumcloser be the closest reachable number to half the sum and partition are sum-halfsumcloser and halfsumcloser.

4.start from halfsum and decrease halfsumcloser once everytime until you find that sol[halfsumcloser] is true