Problem: You are given n types of coins with values {v1,…..,vn} and a cost C. You may assume v1 = 1 so that it is always possible to make any cost. Give an algorithm for finding the smallest number of coins required to sum to C exactly.
For example, assume you coins of values 1, 5, and 10. Then the smallest number of coins to make 26 is 4: 2 coins of value 10, 1 coin of value 5, and 1 coin of value 1.
Solution:
Recursion: We recurse on M(j), the minimum number of coins required to make change for cost j.
Running Time: M has C elements and computing each element takes O(n) time so the total running time is O(nC).
Working code:

All Possible Solutions


Optimal Solution
The optimal solution to this program can be found by using dynamic programming and its runtime can be considerably reduced by a technique called memoization.

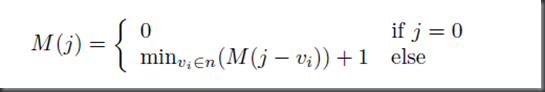










No comments:
Post a Comment