range sum query

Given an array arr[0 . . . n-1]. We should be able to
1 Find the sum of elements from index l to r where 0 <= l <= r <= n-1
2 Change value of a specific element of the array arr[i] = x where 0 <= i <= n-1.

A simple solution is to run a loop from l to r and calculate sum of elements in given range. To update a value, simply do arr[i] = x. The first operation takes O(n) time and second operation takes O(1) time.

Another solution is to create another array and store sum from start to i at the ith index in this array. Sum of a given range can now be calculated in O(1) time, but update operation takes O(n) time now. This works well if the number of query operations are large and very few updates.

Another approach is <O(N), O(sqrt(N))> solution
An interesting idea is to split the vector in sqrt(N) pieces. We will keep in a vector M[0, sqrt(N)-1] the sum of the values of each section.

Group the input by chunks of O(n^1/2), and store the sum of each (chunk 0: sum of arr[0] through arr[sqrt(n)-1]; chunk 1: sum of arr[sqrt(n)] through arr[2*sqrt(n)-1]; etc.). That's your preprocessing step.
Now, each query is the sum of some number (maybe 0) of complete chunks of size O(n^1/2) plus possibly parts of the two chunks on each end of the range. There are at most O(n^1/2) complete chunks to sum that are part of the range. Now consider the two chunks that are partially covered by the range. Each of these 2 chunks has at most O(n^1/2) numbers, so we can just add the individual numbers to the total and still keep the time within O(n^1/2).

Another approach is using segment trees

We can use a Segment Tree to do both operations in O(Logn) time.

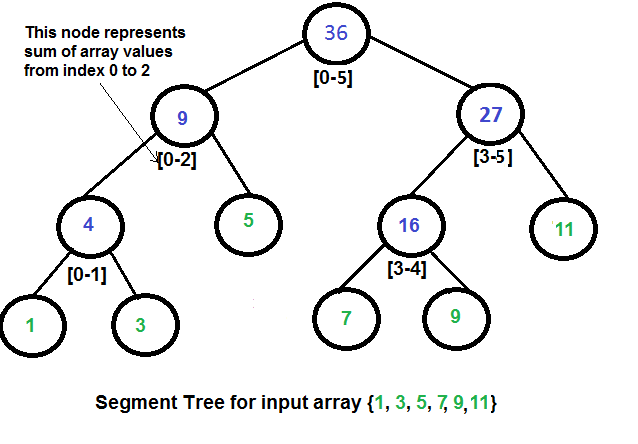
Representation of Segment trees
1. Leaf Nodes are the elements of the input array.
2. Each internal node represents some merging of the leaf nodes. The merging may be different for different problems. For this problem, merging is sum of leaves under a node.

An array representation of tree is used to represent Segment Trees. For each node at index i, the left child is at index 2*i+1, right child at 2*i+2 and the parent is at (i-1)/2.

Query for Sum of given range
Once the tree is constructed, how to get the sum using the constructed segment tree. Following is algorithm to get the sum of elements.

int getSum(node, l, r) 
{
   if range of node is within l and r
        return value in node
   else if range of node is completely outside l and r
        return 0
   else
    return getSum(node's left child, l, r) + 
           getSum(node's right child, l, r)
}

Update a value


Like tree construction and query operations, update can also be done recursively. We are given an index which needs to updated. Let diff be the value to be added. We start from root of the segment tree, and add diff to all nodes which have given index in their range. If a node doesn’t have given index in its range, we don’t make any changes to that node.

References :

http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=lowestCommonAncestor

http://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/

http://www.cse.iitk.ac.in/users/aca/lop12/slides/06.pdf